一般化双曲型分布

一般化双曲型分布（いっぱんかそうきょくがたぶんぷ、英: generalized hyperbolic distribution, GH）は、一般化逆ガウス分布（GIG分布）による正規分散平均混合として定義される連続確率分布で、1977年にBarndoroff-Nielsenにより導入された。GH分布は金融市場のモデル化によく使われている。

一次元一般化双曲型分布

確率密度関数

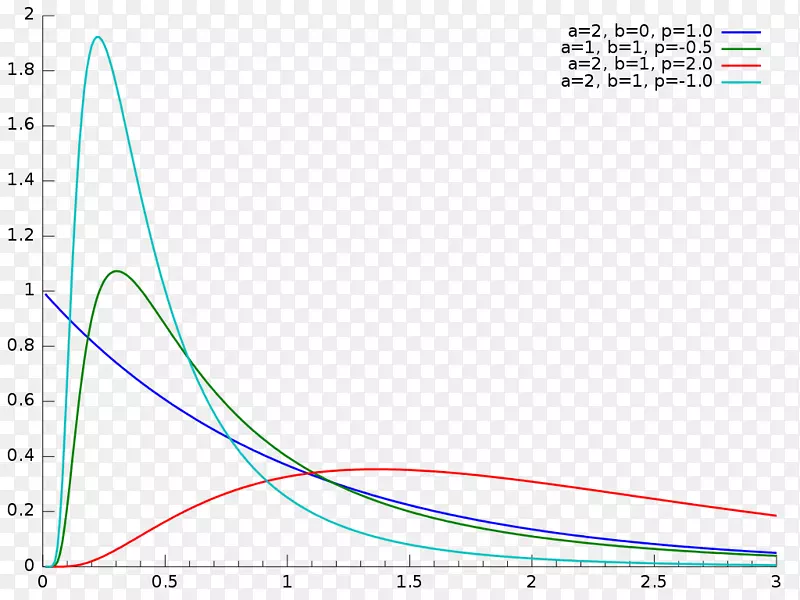
一般化双曲型分布の確率密度関数は以下の式で与えられる。

${\displaystyle {\begin{aligned}gh(x;\lambda ,\alpha ,\beta ,\delta ,\mu )=&a(\lambda ,\alpha ,\beta ,\delta ,\mu )(\delta ^{2} (x-\mu )^{2})^{(\lambda -{\frac {1}{2}})/2}\\&\times K_{\lambda -1/2}(\alpha {\sqrt {\delta ^{2} (x-\mu )^{2}}})\exp(\beta (x-\mu ))\end{aligned}}}$

ここで、

${\displaystyle a(\lambda ,\alpha ,\beta ,\delta ,\mu )={\frac {(\alpha ^{2}-\beta ^{2})^{\lambda /2}}{{\sqrt {2\pi }}\alpha ^{\lambda -1/2}\delta ^{\lambda }K_{\lambda }(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}})}}}$

K_λ(x) は、第3種の変形ベッセル関数。

${\displaystyle \mu }$ 位置 (location) パラメータ（実数）

${\displaystyle \lambda }$ （実数）

${\displaystyle \alpha }$ （実数）

${\displaystyle \beta }$ 歪度 (skewness) /非対称性 (asymmetry) パラメータ（実数）

${\displaystyle \delta }$ 尺度 (scale) パラメータ（実数）

${\displaystyle x\in (-\infty ; \infty )}$

λ > 0 のとき、${\displaystyle \delta \geq 0,\;|\beta |<\alpha }$

λ = 0 のとき、${\displaystyle \delta >0,\;|\beta |<\alpha }$

λ < 0 のとき、${\displaystyle \delta >0,\;|\beta |\leq \alpha }$

モーメント

本節では、以下

${\displaystyle {\begin{aligned}\zeta _{u}&=\delta {\sqrt {\alpha ^{2}-(\beta u)^{2}}}\\\zeta &=\zeta _{u=0}\end{aligned}}}$

とする。

期待値

期待値は以下の式で与えられる。

${\displaystyle {\begin{aligned}E(X)&=\mu {\frac {\delta \beta }{\sqrt {\alpha ^{2}-\beta ^{2}}}}{\frac {K_{\lambda 1}(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}})}{K_{\lambda }(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}})}}\\[0.5em]&=\mu {\frac {\delta ^{2}\beta }{\zeta }}{\frac {K_{\lambda 1}(\zeta )}{K_{\lambda }(\zeta )}}\end{aligned}}}$

分散

分散は以下の式で与えられる。

${\displaystyle {\begin{aligned}\operatorname {Var} (X)&={\frac {\delta }{\sqrt {\alpha ^{2}-\beta ^{2}}}}{\frac {K_{\lambda 1}(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}})}{K_{\lambda }(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}})}} {\frac {\delta ^{2}\beta ^{2}}{(\alpha ^{2}-\beta ^{2})}}\left[{\frac {K_{\lambda 2}(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}})}{K_{\lambda }(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}})}}-\left({\frac {K_{\lambda 1}(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}})}{K_{\lambda }(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}})}}\right)^{2}\right]\\&={\frac {\delta ^{2}}{\zeta }}{\frac {K_{\lambda 1}(\zeta )}{K_{\lambda }(\zeta )}} {\frac {\delta ^{4}\beta ^{2}}{\zeta ^{2}}}\left[{\frac {K_{\lambda 2}(\zeta )}{K_{\lambda }(\zeta )}}-\left({\frac {K_{\lambda 1}(\zeta )}{K_{\lambda }(\zeta )}}\right)^{2}\right]\end{aligned}}}$

モーメント母関数

モーメント母関数は以下の式で与えられる。

${\displaystyle {\begin{aligned}M_{GH}(u)&=\exp(u\mu )\left({\frac {\alpha ^{2}-\beta ^{2}}{(\alpha ^{2}-(\beta u)^{2})}}\right)^{\lambda /2}{\frac {K_{\lambda }(\delta {\sqrt {\alpha ^{2}-(\beta u)^{2}}})}{K_{\lambda }(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}})}}\\[0.5em]&=\exp(u\mu )\left({\frac {\zeta }{\zeta _{u}}}\right)^{\lambda }{\frac {K_{\lambda }(\zeta _{u})}{K_{\lambda }(\zeta )}}\end{aligned}}}$

特性関数

特性関数は以下の式で与えられる。

${\displaystyle \varphi (u)=\exp(iu\mu )\left({\frac {\alpha ^{2}-\beta ^{2}}{(\alpha ^{2}-(\beta iu)^{2})}}\right)^{\lambda /2}{\frac {K_{\lambda }(\delta {\sqrt {\alpha ^{2}-(\beta iu)^{2}}})}{K_{\lambda }(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}})}}}$

特別なケース

λ = 1 の場合

双曲型分布 (HYP) となる。導出には、ベッセル関数の性質を利用する。

確率密度関数

${\displaystyle {\begin{aligned}gh(x;1,\alpha ,\beta ,\delta ,\mu )&=\mathrm {hyp} (x;\alpha ,\beta ,\delta ,\mu )\\&={\frac {\sqrt {\alpha ^{2}-\beta ^{2}}}{2\delta \alpha K_{1}(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}})}}\exp(-\alpha {\sqrt {\delta ^{2} (x-\mu )^{2}}} \beta (x-\mu ))\end{aligned}}}$

λ=1, α=1, β=0, δ=0 の場合はラプラス分布 Laplace(μ, 1) となる。

λ = −1/2 の場合

正規逆ガウス分布 (NIG) となる。導出には、ベッセル関数の性質を利用する。

確率密度関数

${\displaystyle {\begin{aligned}gh(x;-1/2,\alpha ,\beta ,\delta ,\mu )&=\operatorname {nig} (x;\alpha ,\beta ,\delta ,\mu )\\&={\frac {\alpha \delta }{\pi }}\exp(\delta {\sqrt {\alpha ^{2}-\beta ^{2}}} \beta (x-\mu )){\frac {K_{1}(\alpha {\sqrt {\delta ^{2} (x-\mu )^{2}}})}{\sqrt {\delta ^{2} (x-\mu )^{2}}}}\end{aligned}}}$

λ = −1/2, α = β =0 の場合

正規逆ガウス分布 (NIG) の特別な場合として、コーシー分布となる。

λ = −ν/2, α → |β| の場合

自由度 ν の非対称なスチューデントのt分布となる。(β ≠ 0)

${\displaystyle {\begin{aligned}gh(x;&\lambda ={\frac {-\nu }{2}},\alpha \to |\beta |,\beta ,\delta ,\mu )\\&={\frac {\delta ^{\nu }|\beta |^{(\nu 1)/2}K_{(v 1)/2}\left({\sqrt {(\delta ^{2} (x-\mu )^{2})\beta ^{2}}}\right)\exp(\beta (x-\mu ))}{2^{(v-1)/2}\Gamma \left({\frac {\nu }{2}}\right){\sqrt {\pi }}\left({\sqrt {\delta ^{2} (x-\mu )^{2}}}\right)^{(\nu 1)/2}}}\end{aligned}}}$

λ = −ν/2, α = β = 0, δ = √ν の場合

自由度 ν の（対称な）スチューデントのt分布となる。

${\displaystyle {\begin{aligned}gh(x;&\lambda ={\frac {-\nu }{2}},\alpha =0,\beta =0,\delta ={\sqrt {\nu }},\mu )\\&={\frac {\Gamma \left({\frac {\nu 1}{2}}\right)}{{\sqrt {\pi }}\delta \Gamma \left({\frac {\nu }{2}}\right)}}\left[1 {\frac {(x-\mu )^{2}}{\delta ^{2}}}\right]^{-{\frac {\nu 1}{2}}}\\&={\frac {\Gamma \left({\frac {\nu 1}{2}}\right)}{{\sqrt {\pi \nu }}\Gamma \left({\frac {\nu }{2}}\right)}}\left(1 {\frac {(x-\mu )^{2}}{\nu }}\right)^{-{\frac {\nu 1}{2}}}\end{aligned}}}$

α → ∞, δ → ∞, δ/α → σ² の場合

平均 μ βσ²、分散 σ² の正規分布となる。

参考文献

（英語）

• The Generalized Hyperbolic Model: Estimation, Financial Derivatives, and Risk Measures (PDF) , Karsten Prause, Oktober 1999.
• Generalized Hyperbolic and Inverse Gaussian Distributions: Limiting Cases and Approximation of Processes (PDF) , Ernst Eberlein and Ernst August v. Hammerstein, revised April 2003.
• Absolute moments of generalized hyperbolic distributions and approximate scaling of normal inverse Gaussian Lévy-Processes (PDF) , Ole Eiler Barndorff-Nielsen and Robert Stelzer, April 25, 2004.
• Moments of the Generalized Hyperbolic Distribution(PDF), David Scott, Department of Statistics, The University of Auckland, July 3, 2008.
• Moments of the Generalized Hyperbolic Distribution (PDF) , Scott, David J, Wurtz, Diethelm, Dong, Christine and Tran,

Thanh Tam, Dec 09, 2009.

（日本語）

• GIG分布とGH分布に関する解析 (PDF) 、増田 弘毅、統計数理 (2002) 第 50 巻 第 2 号 165–199 ©2002 統計数理研究所 特集「ファイナンス統計学」

脚注

^a b  ${\displaystyle K_{-{\frac {1}{2}}}(x)=K_{\frac {1}{2}}(x)={\sqrt {\frac {\pi }{2}}}x^{-{\frac {1}{2}}}\exp(-x)}$

外部リンク

• Wolfram Demonstration Project - Generalized Hyperbolic Distribution（GH確率密度関数のグラフを見ることができる。）